De la vapeur aux algorithmes, une même idée relie le désordre des atomes et les messages que nous envoyons chaque jour : l’entropie.

Quand le désordre devient une loi

Imaginez un parfum que l’on vaporise dans une pièce. Au début, les molécules se concentrent près du flacon ; quelques secondes plus tard, elles se sont dispersées partout.
Rien d’étonnant à cela, et pourtant, ce simple phénomène contient une loi universelle : le désordre tend à croître [1].

Ce principe, formulé au XIXᵉ siècle par les pionniers de la thermodynamique, s’appelle la deuxième loi de la thermodynamique : dans un système isolé, l’entropie ne diminue jamais.
Autrement dit, les processus spontanés sont ceux qui augmentent le désordre global.

Mais que signifie exactement cette mystérieuse “entropie” ? Est-ce seulement une grandeur qui décrit un système physique comme un gaz, ou une notion plus universelle ?
Pour répondre à cette question, il faut chercher les liens entre probabilité, physique et information.

Figure 1 – Diffusion d’un parfum dans l’air
Illustration : les molécules passent d’un état ordonné (concentrées) à un état désordonné (réparties uniformément), symbole de l’augmentation de l’entropie.

Boltzmann : le hasard des atomes

Vers 1870, le physicien autrichien Ludwig Boltzmann cherche à expliquer les lois de la chaleur à partir du comportement microscopique de milliards d’atomes.
Il introduit alors une célèbre formule [2]:

S=k lnW

où S est l’entropie,  W le nombre de configurations microscopiques possibles correspondant à un même état macroscopique et k celle que le physicien Max Planck appela la constante de Boltzmann et qui relie la température d’un système à l’énergie moyenne de ses particules microscopiques [3].

Plus un état peut être réalisé de façons différentes, plus il est probable et plus son entropie est grande. L’équilibre thermique — quand tout paraît “mélangé” — est en fait l’état le plus probable, celui qui maximise le désordre, car il correspond au nombre maximal des configurations.

On peut dire que les systèmes évoluent vers les états les plus nombreux et que l’entropie marque la direction dans laquelle les systèmes évoluent naturellement. Ainsi, la flèche du temps n’est pas imposée par une loi fondamentale, mais par la probabilité.

Figure 2 – Pierre tombale de Ludwig Boltzmann (1844–1906)
avec un buste du physicien et sa formule d’entropie. (Source: Wikimedia Commons)

Shannon : du hasard des atomes au hasard des messages

Presque un siècle plus tard, le mathématicien Claude Shannon, s’inspire de Boltzmann pour quantifier une tout autre forme d’incertitude : celle des messages.

En 1948, il publie A Mathematical Theory of Communication [4] et introduit une formule d’apparence jumelle :

H=−∑_i p_i log₂ p_i

où H mesure la quantité moyenne d’information d’une source qui émet des symboles avec des probabilités pi.
Quand tout est imprévisible (par exemple quand la probabilité de tirer pile ou face est 0,5), l’entropie est maximale ; quand tout est connu d’avance, elle est nulle.

L’entropie de Shannon ne mesure pas le désordre matériel, mais l’incertitude d’un message.
Et pourtant, les deux notions sont liées : dans les deux cas, l’entropie quantifie le nombre de possibles.

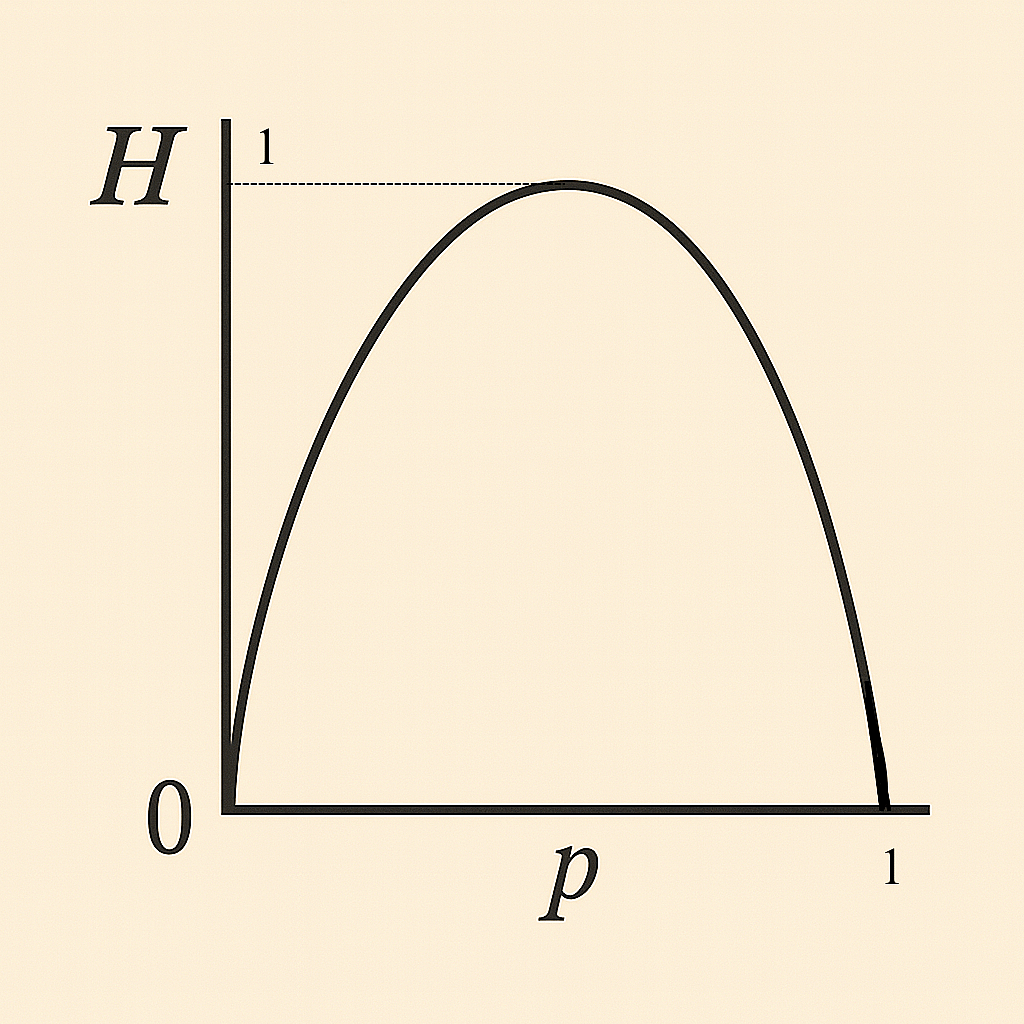
 Figure 3 – Entropie de Shannon en fonction de la probabilité

La courbe représente l’entropie binaire H(p)=−p log₂p − (1−p) log₂(1−p), qui mesure l’incertitude moyenne associée à un événement aléatoire prenant deux valeurs possibles avec probabilités p et 1−p.
L’entropie est minimale pour p=0 ou p=1, car l’une des deux issues est certaine : le système ne comporte plus d’aléa et l’observation n’apporte aucune information nouvelle. Elle est maximale pour p=0,5, lorsque les deux issues sont équiprobables ; dans ce cas, la prévisibilité est nulle et chaque observation transmet en moyenne un bit d’information. Cette forme symétrique traduit ainsi la correspondance directe entre incertitude maximale et contenu informationnel maximal.

La correspondance est plus profonde qu’une simple analogie. Le physicien John von Neumann aurait conseillé à Shannon :

“Appelez votre mesure ‘entropie’. Personne ne sait vraiment ce que c’est, donc dans une discussion, vous aurez toujours l’avantage.”

Au-delà de la plaisanterie, les deux entropies obéissent à des lois semblables.
Effacer de l’information, c’est augmenter le désordre ; stocker de l’information, c’est créer de l’ordre — mais à un coût.

En 1961, Rolf Landauer démontre qu’effacer un seul bit d’information nécessite une énergie minimale [5]:

E_min =kT ln2

où T est la température absolue.
Autrement dit, l’information a un prix énergétique. C’est le lien direct entre le monde des bits et celui des atomes.

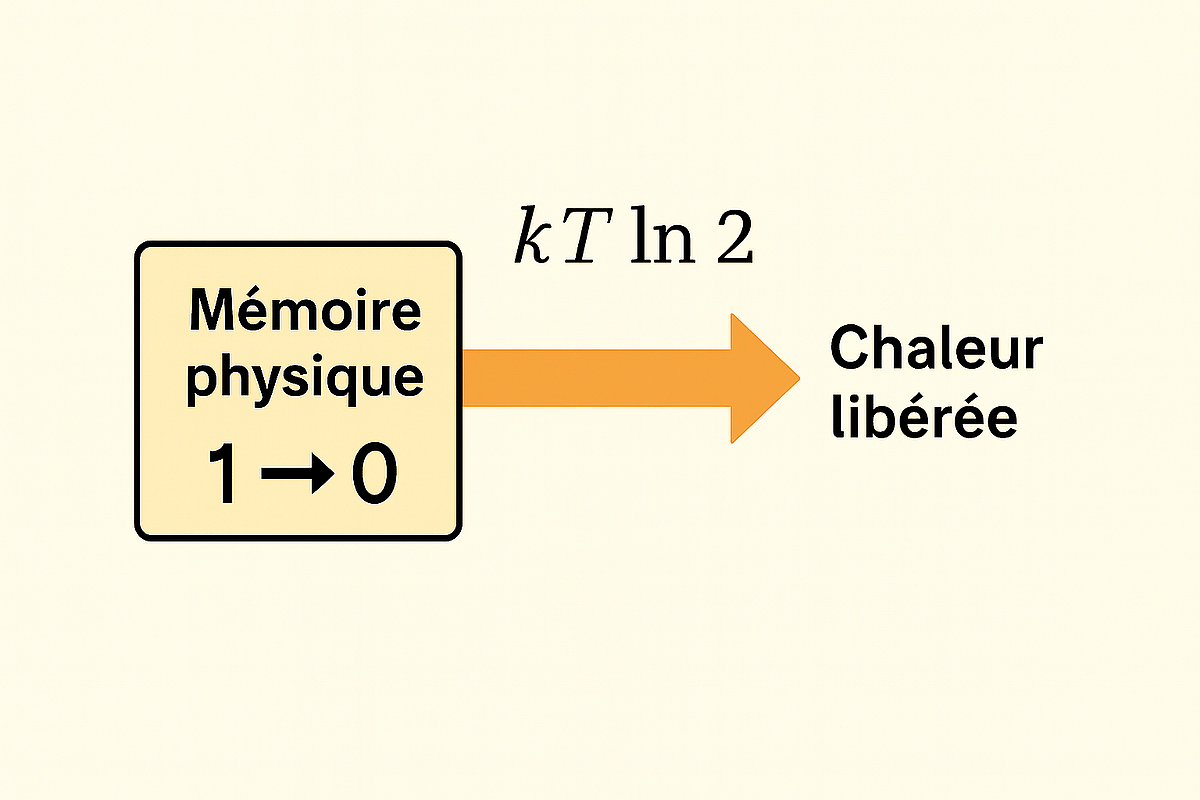
Figure 4 – Schéma de la limite de Landauer
Effacer un bit dans une mémoire physique libère inévitablement une chaleur minimale kTln2.

Et on ne s’arrête pas là. 

Dans les années 1970, Jacob Bekenstein et Stephen Hawking ont montré qu’un trou noir possède une entropie proportionnelle à la surface de son horizon — et non à son volume !
Cette “entropie de Bekenstein-Hawking” relie la gravitation, la mécanique quantique et la thermodynamique [6], [7]. Là encore, l’information n’est jamais perdue : elle se cache, codée dans la géométrie de l’espace-temps.

L’entropie au quotidien

Si ces idées semblent cosmiques, elles régissent pourtant notre vie de tous les jours.

• Compression d’images et de sons : les formats JPEG ou MP3 utilisent l’entropie pour éliminer les redondances. Moins un signal est prévisible, plus il contient d’information [8].
• Météorologie : prévoir le temps, c’est réduire l’entropie d’un système chaotique [9].
• Biologie : le génome, loin d’être un simple code, contient une mesure d’ordre face à la diversité des mutations possibles.
• Écologie : certains indicateurs de biodiversité s’inspirent directement de la formule de Shannon.

Même nos sociétés numériques reposent sur la gestion du désordre : protéger nos données, c’est maintenir de l’ordre dans un océan d’incertitude.

Figure 6 – Applications de l’entropie dans la vie quotidienne
Exemples : compression JPEG, météo, génétique, biodiversité. Le même concept mesure le désordre sous des formes multiples.

Entropie, incertitude et créativité

On pourrait croire que l’entropie est l’ennemie de la vie ou de l’intelligence.
Pourtant, c’est souvent l’équilibre entre ordre et désordre qui permet la complexité.
Un système totalement ordonné est figé ; un système totalement chaotique est imprévisible.
La vie, comme la pensée, prospère à la frontière entre les deux. 

L’entropie est ainsi un fil conducteur entre les disciplines.
Elle révèle comment les mathématiques traduisent le hasard en structure.

Derrière le chaos apparent, l’entropie dessine donc une forme d’ordre — celui de la probabilité.

[1] Clausius, R. (1865). Über verschiedene für die Anwendung bequeme Formen der Hauptgleichungen der mechanischen Wärmetheorie. Annalen der Physik und Chemie, 201(7), 353–400.
[2] Boltzmann, L. (1877). Über die Beziehung zwischen dem zweiten Hauptsatze der mechanischen Wärmetheorie und der Wahrscheinlichkeitsrechnung. Sitzungsberichte der Kaiserlichen Akademie der Wissenschaften, 76, 373–435.
[3] BIPM (2019). Le Système international d’unités (SI) — redéfinition : valeur exacte de la constante de Boltzmann http://www.w3.org/1998/Math/Ma...">kk= 1,380 649×10⁻²³ J·K⁻¹. (Note métrologique / CODATA 2018–2019.)
[4] Shannon, C. E. (1948). A Mathematical Theory of Communication. Bell System Technical Journal, 27, 379–423 & 623–656.
[5] Landauer, R. (1961). Irreversibility and Heat Generation in the Computing Process. IBM Journal of Research and Development, 5(3), 183–191.                                                         [6] Bekenstein, J. D. (1973). Black Holes and Entropy. Physical Review D, 7(8), 2333–2346.
[7] Hawking, S. W. (1975). Particle Creation by Black Holes. Communications in Mathematical Physics, 43, 199–220.
[8] Wallace, G. K. (1992). The JPEG Still Picture Compression Standard. Communications of the ACM, 34(4), 30–44.
[9] Lorenz, E. N. (1963). Deterministic Nonperiodic Flow. Journal of the Atmospheric Sciences, 20(2), 130–141.