Flot et fluctuations: explorer la collectivité dans les collisions d’ions lourds
Publié par Victor Valencia Torres, le 6 octobre 2025 330
La matière ordinaire repose sur une structure fondamentale composée de quarks et de gluons, décrite par la chromodynamique quantique (QCD). Six « saveurs » de quarks sont connues : up, down, strange, charm, bottom et top.
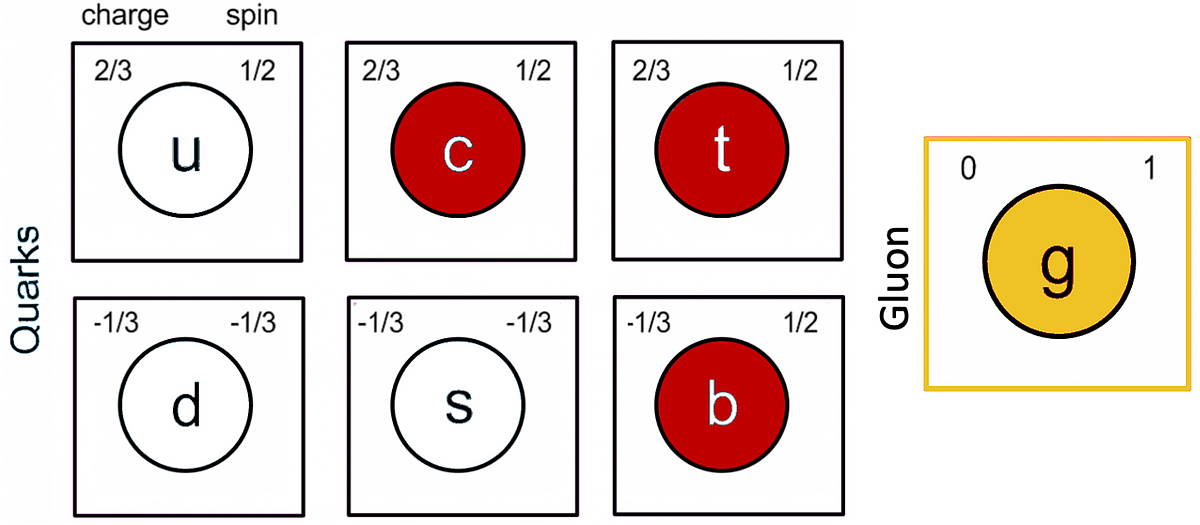
Dans des conditions normales, les quarks ne sont jamais observés isolés : ils sont confinés dans des états liés appelés hadrons. Ces derniers se répartissent en deux grandes familles :
- Les baryons (comme le proton et le neutron), constitués de trois quarks.
- Les mésons, formés d’un quark et d’un antiquark.
Pour étudier les propriétés des quarks libérés de ce confinement, les physiciens recréent des conditions extrêmes similaires à celles de l’Univers primordial. Grâce au Large Hadron Collider (LHC) du CERN [1], ils font entrer en collision des noyaux lourds à des vitesses proches de celle de la lumière.
Ces collisions produisent un état de la matière extrêmement chaud et dense, appelé plasma de quarks et de gluons (QGP). Dans ce milieu, les quarks et les gluons se déplacent librement pendant un court instant, formant un fluide fortement couplé. À mesure que le système se refroidit, ils se recombinent pour former de nouveaux hadrons détectables — un processus appelé hadronisation.
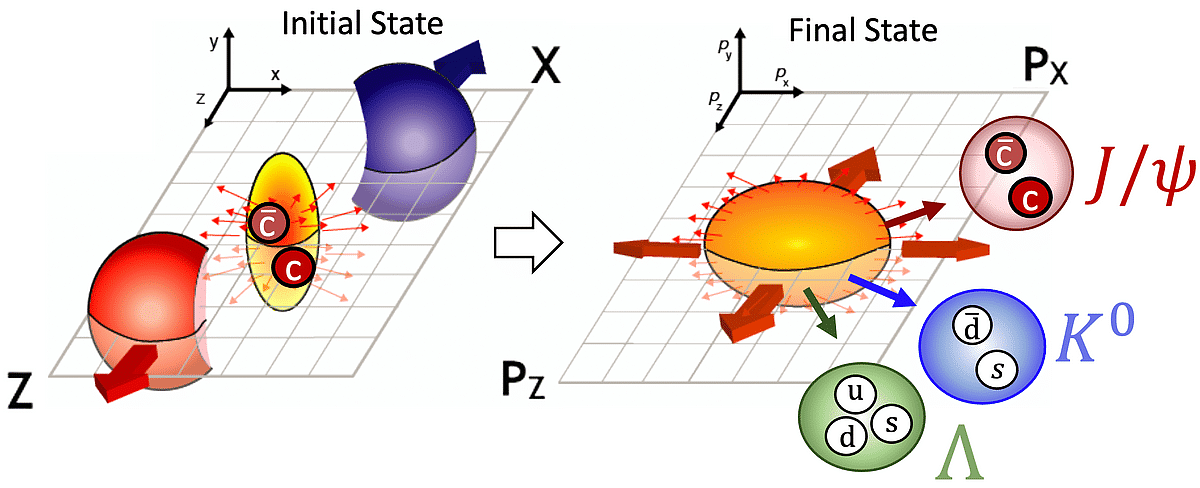
Le J/ψ, par exemple, est un méson composé d’un quark charm et d’un antiquark charm. Comme ces quarks sont produits très tôt dans la collision, leur comportement collectif fournit des informations précieuses sur la thermalisation des quarks lourds dans le QGP.
Flot anisotropique
Pour sonder les propriétés de ce plasma, plusieurs observables sont utilisées. Parmi elles, les corrélations azimutales entre particules sont essentielles pour étudier la collectivité du QGP.
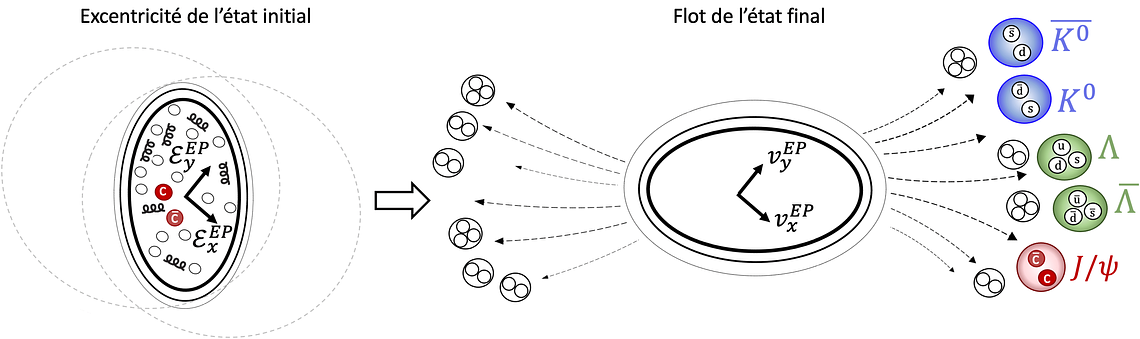
Lors d’une collision, la zone de recouvrement entre les deux noyaux présente souvent une forme en amande. Cette géométrie initiale engendre une expansion anisotrope du plasma, qui se manifeste dans la distribution en angle azimutal des particules émises. Grâce à la périodicité de cette forme, on peut développer cette distribution en série de Fourier :
Ce développement en série de Fourier décrit la distribution des particules dans le plan transverse. Les coefficients de Fourier vn quantifient le degré d’anisotropie du flux de particules.
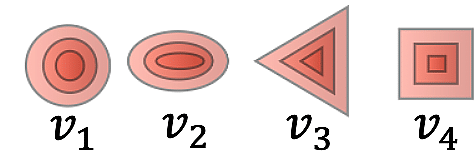
Le flot elliptique joue un rôle central : il reflète la réponse hydrodynamique du plasma. Des valeurs élevées indiquent un fluide à faible viscosité, proche d’un fluide parfait.
Le détecteur ALICE : une caméra tridimensionnelle du QGP
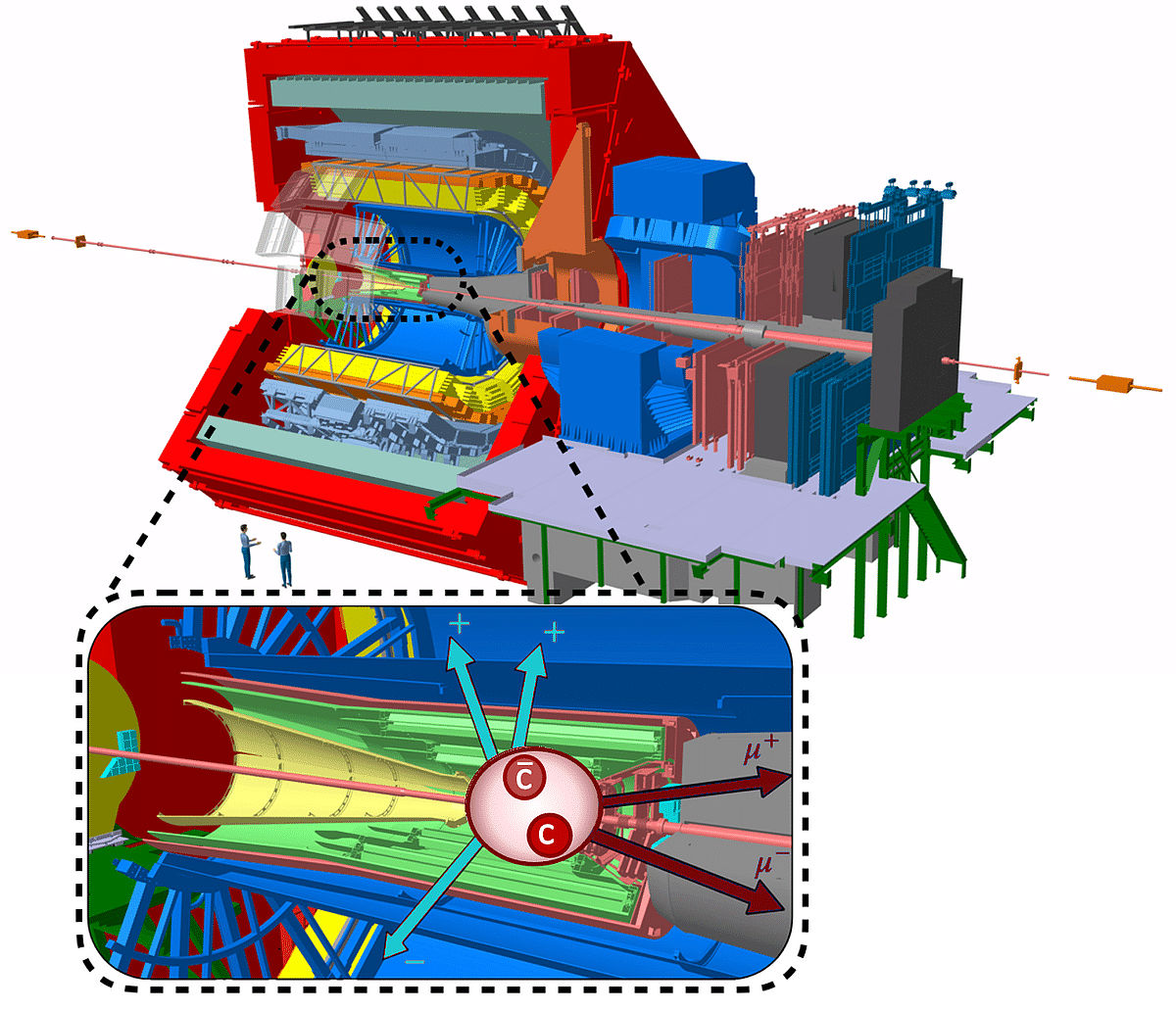
|
Le détecteur ALICE (A Large Ion Collider Experiment) [3] est conçu pour enregistrer les trajectoires des particules produites à chaque collision. Les flèches visibles dans la Figure 4 correspondent principalement à des particules chargées. Leur analyse est essentielle pour mesurer les corrélations azimutales et extraire les coefficients de flot. Pour déterminer ces coefficients de manière fiable, les physiciens utilisent des cumulants multiparticules, qui isolent les contributions collectives en réduisant les corrélations non collectives. Dans notre cas, on corrèle des dimuons à l’avant (issus de la décroissance du J/ψ) avec des traces chargées dans la partie centrale du détecteur. |
Résultats : flot et fluctuations événement par événement
Pour une géométrie initiale similaire, la distribution microscopique des nucléons (à l’intérieur de l’amande) fluctue d’un événement à l’autre [4]. Cela peut induire des variations du flot appelées fluctuations du flot. En exploitant les différences entre les corrélations à deux et à quatre particules, on peut étudier ces fluctuations [5], notées σ.
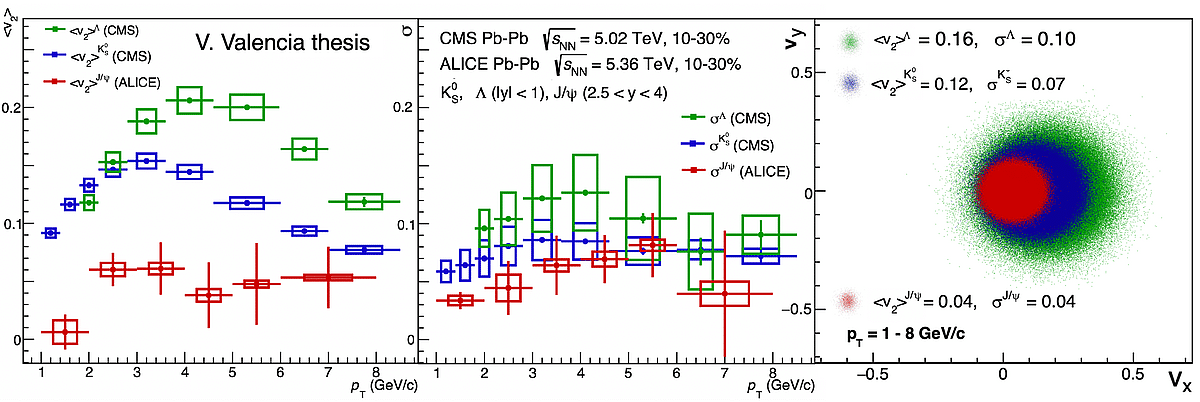
Les hadrons légers (KS0 et Λ), mesurés par la collaboration CMS [6], présentent des valeurs de v2 élevées, signe d’un fort couplage des quarks légers au QGP. Pour les hadrons contenant des quarks lourds, comme le J/ψ mesuré par ALICE, on observe des valeurs plus faibles, comme attendu en raison de la masse importante des quarks charm.
Un v2 non nul pour les J/ψ constitue une preuve claire que même les sondes lourdes sont entraînées par le flux collectif — un résultat d’autant plus remarquable que les fluctuations jouent ici un rôle significatif.
Ces avancées approfondissent notre compréhension des effets collectifs dans la matière fortement couplée et permettent de tester la QCD dans des conditions proches de celles qui régnaient peu après le Big Bang.
Références
- O. S. Bruning, P. Collier, P. Lebrun, S. Myers, R. Ostojic, J. Poole et P. Proudlock (éds.), LHC Design Report Vol. 1: The LHC Main Ring, CERN, juin 2004. DOI : 10.5170/CERN-2004-003-V-1.
- J.-Y. Ollitrault, “Anisotropy as a signature of transverse collective flow,” Phys. Rev. D, vol. 46, pp. 229–245, 1992. DOI : 10.1103/PhysRevD.46.229.
- K. Aamodt et al., “The ALICE experiment at the CERN LHC,” JINST, vol. 3, S08002, 2008. DOI : 10.1088/1748-0221/3/08/S08002.
- S. Manly, “System size, energy and pseudorapidity dependence of directed and elliptic flow at RHIC,” Nuclear Physics A, vol. 774, pp. 523–526, août 2006. DOI : 10.1016/j.nuclphysa.2006.06.079.
- S. A. Voloshin, A. M. Poskanzer, A. Tang et G. Wang, “Elliptic flow in the Gaussian model of eccentricity fluctuations,” Physics Letters B, vol. 659, no. 3, pp. 537–541, janv. 2008. DOI : 10.1016/j.physletb.2007.11.043.
- CMS Collaboration, “Strange hadron collectivity in pPb and PbPb collisions,” JHEP, vol. 2023, no. 5, p. 007, mai 2023. DOI : 10.1007/JHEP05(2023)007.