Cet article traite de certaines avancées expérimentales et théoriques récentes dans notre compréhension de l’interaction forte. Celle-ci est l’une des quatre interactions fondamentales de la nature, aux côtés de la gravitation, de l’interaction électromagnétique et de l’interaction faible, qui régissent l’ensemble des phénomènes physiques connus à ce jour. L’interaction forte joue un rôle central dans la stabilité de la matière, laquelle, rappelons-le, est constituée d’atomes.

Quark et gluon

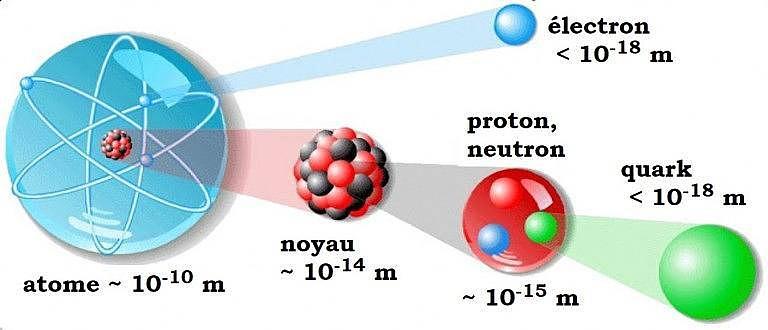
Un atome se compose d’un noyau, qui concentre l’essentiel de sa masse, entouré d’électrons beaucoup plus légers, responsables quant à eux de ses propriétés chimiques. Le noyau est lui-même un assemblage de protons et de neutrons, que l’on regroupe sous le nom de nucléons. Ce qui maintient ces nucléons liés entre eux, malgré la répulsion électrique entre protons, c’est précisément l’interaction forte. Sans elle, les noyaux atomiques seraient instables et les atomes, tels que nous les connaissons, n’existeraient pas.

Pour comprendre les phénomènes physiques à l’échelle des nucléons, les physicien·nes adoptent une approche réductionniste : en établissant les lois à l'échelle des éléments premiers les plus fondamentaux, on détermine les lois et les propriétés du tout. Ainsi, les protons et neutrons ne sont pas des objets élémentaires, mais des systèmes composés de particules plus fondamentales encore, les quarks, liés entre eux par la particule médiatrice de l'interaction forte appelée gluon (car elle agit comme une colle extrêmement puissante pour garantir la stabilité des nucléons). Cette description s’applique à des échelles de distance extrêmement petites, de l’ordre de 10^(−15) mètre, soit environ cent mille fois plus petites que la taille caractéristique d’un atome. En élucidant les lois régissant les quarks et les gluons et en comprenant comment ces derniers s'organisent pour former des nucléons, nous sommes ainsi en mesure d'expliquer leurs propriétés globales comme leur masse, leur charge, etc. Cette approche réductionniste s'applique en outre à bien d'autres particules, progressivement découvertes au cours de la seconde moitié du XXe siècle (comme les pions, les kaons, etc), que l'on nomme "hadrons" et qui ont la caractéristique d'être aussi constituées de quarks liés entre eux par les gluons.

Comment sonder l'intérieur des nucléons ?

Comme souvent en physique, la structure interne d'un corps est mesurée un utilisant une autre particule "sonde", celle-ci élémentaire, qui en frappant sa cible, en l'occurrence un nucléon, en révèle la structure interne de façon indirecte, en mesurant la déviation de la sonde après la collision. Ainsi, la structure atomique des cristaux s'obtient en bombardant le matériau avec des rayons X, c'est à dire des photons (corpuscule de lumière), et en mesurant comment ces photons sont déviés par le cristal.

Cette idée trouve son fondement dans la mécanique quantique, et la fameuse dualité onde-corpuscule: une particule élémentaire se comporte également comme une onde. Contrairement à un corpuscule, grain de matière sans extension spatiale et synonyme ici de particule, une onde est un objet physique étendu, que l'on se représente comme une série de vagues se propageant dans l'espace. En physique, la distance entre deux crêtes s'appelle la longueur d'onde. La loi de De Broglie de la mécanique quantique stipule que la longueur d'onde de l'onde associée à une particule est d'autant plus petite que l'énergie du corpuscule est grande. 

Or, une onde n'est perturbée au cours de sa propagation que par des corps typiquement plus gros que sa longueur d'onde : un bouchon de liège agité par une houle ne va pas affecter la propagation des vagues, mais un obstacle comme une digue à l'entrée d'un port, oui ! Ainsi, si l'on veut révéler la structure interne des nucléons à des distances de l'ordre de 10^(-15) mètre, il faut percuter les nucléons avec un corpuscule dont la longueur d'onde est inférieure à cette longueur, de façon à ce que le corpuscule "sonde" soit perturbé par son interaction avec la cible. De telles longueurs d'onde extrêmement petites correspondent ainsi à des énergies colossales pour une particule, supérieures à 10^9 eV. En physique, 1 eV est l'énergie d'un électron soumis à une différence de potentiel électrique de 1 Volt. A titre de comparaison, l'énergie typique d'un électron autour d'un noyau atomique est de l'ordre de la dizaine d'eV. Les énergies qui doivent être mises en jeu sont donc au moins 100 millions de fois plus élevées.

La diffusion électron-proton profondément inélastique

La sonde idéale pour mesurer la structure interne du proton est l'électron, car c'est une particule élémentaire facile à produire, bien que difficile à accélérer à de telles énergies. Ainsi, l'expérience reine de la physique nucléaire haute énergie, nommée "diffusion électron-proton profondément inélastique", consiste à bombarder un proton avec un électron à très haute énergie et à mesurer la déviation de l'électron diffusé après la collision pour en déduire la composition du proton en terme de quarks et gluons.

De telles expériences ont été réalisées pour la première fois à la fin des années 60 au Stanford Linear Accelerator Center (SLAC) aux Etats-Unis. Le collisionneur électron-proton Hadron-Electron Ring Accelerator (HERA, voir image en en-tête de cet article, crédit photo: DESY) situé  à Hambourg, en Allemagne a ensuite pris la relève pour un programme d'étude de précision de la sous-structure du proton entre 1992 et 2007. De nos jours, des collisions électron-proton ont lieu au Jefferson National Laboratory (US) et des collisions muon-proton sont réalisées au CERN avec l'expérience COMPASS (le muon est une sorte d'électron, mais plus massif), dans les deux cas en mode cible fixe. Enfin, à l'horizon 2030, l'Electron-Ion Collider (EIC) devrait entrer en service au Brookhaven National Laboratory aux Etats-Unis et pour la première fois, des collisions entre un faisceau d'électrons et un faisceau de noyaux atomiques composés de plusieurs nucléons seront réalisées, afin de mieux comprendre la structure des noyaux directement en termes des constituants élémentaires que sont les quarks et les gluons [5].

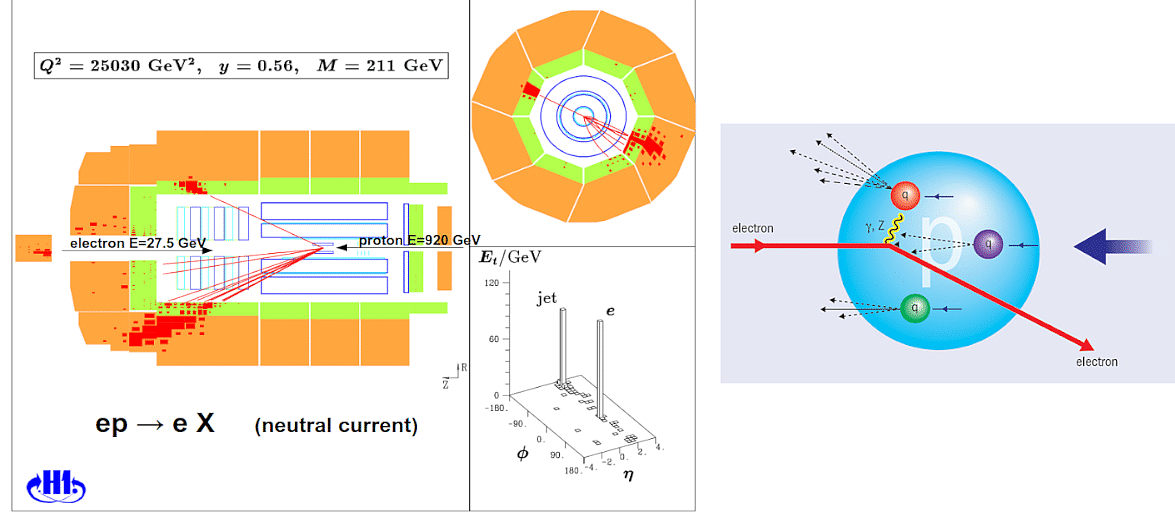
L'héritage d'HERA: structure interne du proton à haute énergie

Cependant, contrairement aux cristaux que l'on sonde par diffraction de rayon X, les nucléons ont une structure interne qui n'est pas figée, elle fluctue en fonction notamment de l'énergie de la sonde elle-même ! En effet, comme expliqué précédemment, plus l'énergie augmente, plus la longueur d'onde de l'électron "sonde" est courte et donc plus la sonde est à même de résoudre des détails plus fins à l'intérieur du nucléon. Cette dépendance en l'énergie de la structure élémentaire du proton a été abondamment étudiée par les expériences H1 et ZEUS du collisionneur HERA. Un résultat expérimental très important est le fait que plus l'énergie de l'électron est grande, plus il va "voir" des gluons à l'intérieur du nucléon. Il y a ainsi prolifération du nombre de gluons dans les nucléons à très haute énergie. La courbe ci-dessous donne la probabilité que l'électron "voit" un quark ou un gluon en fonction de la valeur de x, la variable de Bjorken, qui est inversement proportionnelle à l'énergie de la collision (pour une échelle de résolution transverse fixée). Ainsi, plus x est petit, plus la collision est énergétique. On constate que dans ce régime, c'est comme si le proton était composé essentiellement de gluons, la contribution venant des quarks devenant négligeable.



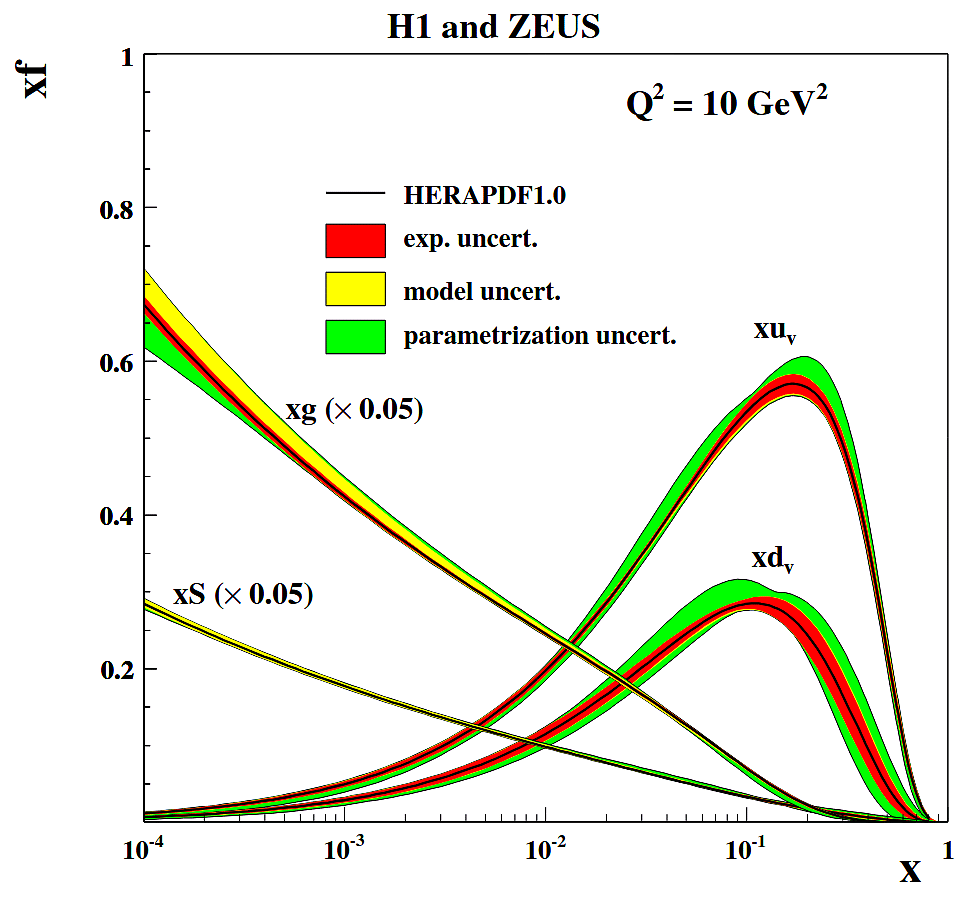
Le nucléon saturé en gluons: le condensat de verre de couleur

Or les gluons sont des particules élémentaires très spéciales: elles interagissent très facilement entre elles. Dans le cadre du modèle standard de la physique des particules, nous l'avons dit, le gluon est la particule médiatrice de l'interaction forte. On peut la comprendre dans un premier temps comme l'équivalent du photon, particule médiatrice de l'interaction électromagnétique, qui soude l'électron et le noyau chargé positivement dans un atome d'hydrogène. Cependant, l'interaction des gluons entre eux rend l'interaction forte, bien plus complexe et fascinante, si l'on compare à l'interaction électromagnétique: deux photons n'interagissent quasiment pas entre eux et en l'absence d'interaction avec la matière, ils peuvent voyager éternellement sans altération, même s'ils se croisent. C'est ainsi que l'on peut mesurer aujourd'hui des photons issus des tous premiers instants de l'Univers, notamment.

Au contraire, un gluon peut aisément émettre (on dit "rayonner") un autre gluon: d'un gluon, on passe alors à deux gluons, et ainsi de suite. C'est l'explication physique de la prolifération des gluons dans les nucléons qui a été mise en évidence par l'accélérateur HERA. Inversement, deux gluons voisins dans un nucléon s'influencent fortement l'un-l'autre ; notamment, ils peuvent se recombiner en un seul gluon, dans un processus appelé fusion de gluons. Ainsi, bien qu'à très haute énergie, le nombre de gluons dans un nucléon augmente, cette prolifération doit en principe ralentir du fait de ce processus de fusion. Une forme d'équilibre dynamique s'installe entre l'accroissement de la densité de gluons par rayonnement, et leur recombinaison par fusion. Se produit alors une transition vers un état de la matière saturé en gluons et que l'on nomme condensat de verre de couleur.

Le "condensat" se réfère ici à la formation d'un état à haute densité de gluons, particules qui comme les quarks, portent une charge dite de "couleur", analogue de la charge électrique pour l'interaction forte. En outre, ce condensat partage des propriétés physiques similaires à celles des verres, d'où sa qualification "vitreuse", en particulier l'existence de deux échelles de temps caractéristiques fortement ordonnées: une échelle de temps très courte associée au temps de vie des gluons copieusement produits à petit x, et une échelle de temps beaucoup plus longue correspondant au temps de vie des charges de couleurs à des valeurs de x plus élevées qui sont les sources émettrices de ces gluons à petit x. Du fait de cette hiérarchie en temps, les sources peuvent être considérées comme figées, quasi-statiques, pendant le temps très bref de l'interaction entre la sonde et un gluon du condensat. Néanmoins, comme dans les verres, il est important de prendre en compte les fluctuations de ces degrés de liberté quasi-statiques d'une collision à une autre.

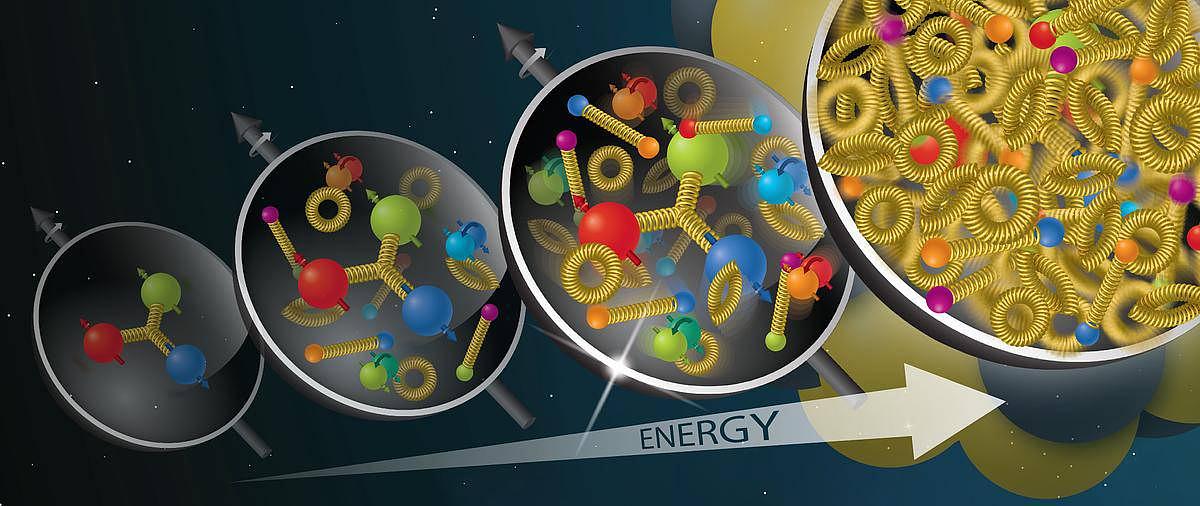
Vers une mesure expérimentale de l'échelle de saturation ?

Un enjeu majeur des expériences actuelles et futures de la physique hadronique et de la physique nucléaire à haute énergie est de mieux comprendre cet état de la matière et de quantifier ses propriétés [7,8]. En l'occurrence, une caractéristique physique essentielle du condensat est l'échelle de saturation, notée Qs. Pour se représenter le sens physique de Qs, il est plus commode d'abandonner momentanément notre "électron-sonde", et de la remplacer par une sonde élémentaire fictive qui, contrairement à l'électron, porterait une charge de couleur, tel un quark. En effet, l'électron en diffusion profondément inélastique n'interagit pas directement avec les gluons du condensat de verre de couleur, car l'électron n'est pas sensible à l'interaction forte, à l'inverse des quarks.  

Cependant, expérimentalement, on ne peut pas produire un faisceau de quark pour faire des collisions idéales quark-nucléon, mais une bonne approximation consiste à utiliser un faisceau de proton, et de s'assurer que la collision sera telle qu'elle n'impliquera qu'un quark à l'intérieur du "proton-sonde". Cela est possible dans les collisions proton-proton ou proton-noyau qui sont réalisées au Grand Collisionneur de Hadron (LHC) situé au CERN, à la frontière franco-suisse ou au Relativistic Heavy-Ion Collider (RHIC) situé au Brookhaven National Laboratory. 

Quand une charge de couleur interagit avec le condensat de verre de couleur, cette dernière va subir une diffusion dans le plan perpendiculaire à l'axe de la collision (comme sur le schéma à gauche ci-dessous) du fait des multiples collisions microscopiques entre cette charge de couleur et les gluons abondamment présents à l'intérieur de la cible. La particule colorée sonde émerge alors du condensat avec une impulsion transverse caractéristique que l'on appelle échelle de saturation Qs.

Cette diffusion peut être pensée par analogie avec le mouvement brownien, le mouvement d'un corps mésoscopique (tel un grain de pollen) dans un liquide, causé par les collisions incessantes entre ce corps et les atomes du liquide en perpétuelle agitation, étudié notamment par Jean Perrin au début du XXeme siècle. Dans un mouvement brownien, la moyenne du carré du déplacement du corps mésoscopique augmente avec le temps. De façon analogue, la moyenne du carré de l'impulsion transverse acquise par la charge de couleur se propageant dans le condensat, qui est donc précisément le carré de l'échelle de saturation, est proportionnelle au temps passé par la charge dans le condensat, et donc aussi proportionnelle à la longueur parcourue. Pour un noyau sphérique contenant A nucléons, le rayon de la sphère est d'ordre A^(1/3) fois la taille d'un nucléon (de l'ordre de 10^(-15) mètre) et donc on s'attend à ce que Qs^2 augmente comme A^(1/3) avec le nombre de nucléon du noyau cible.

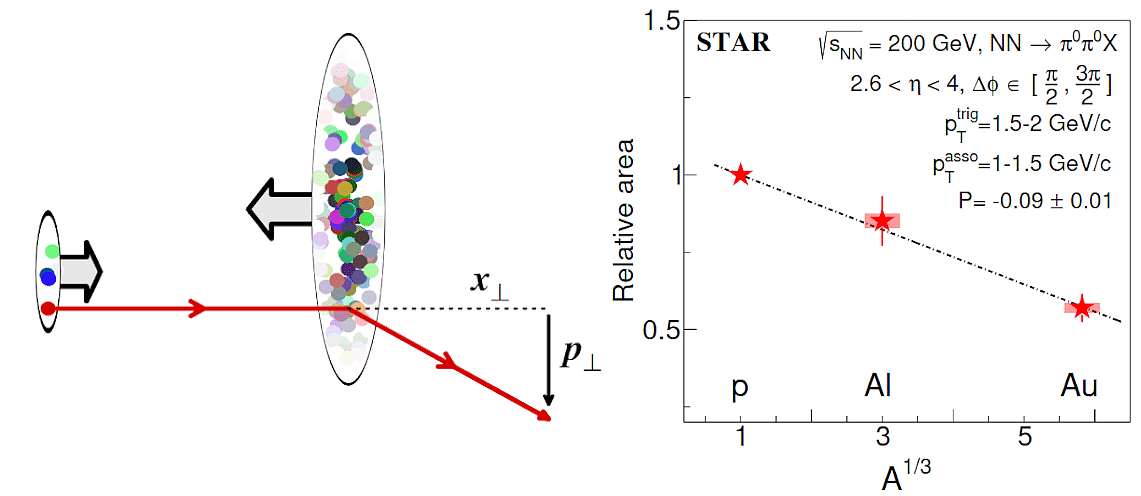
Des mesures récentes réalisées par l'expérience STAR au RHIC en collision proton-noyau semblent confirmer cette loi d'échelle prévue théoriquement qui stipule que Qs^2 augmente comme A^(1/3) (voir [4] et figure ci-dessus à droite). Les physicien·nes travaillent également à concevoir des observables mesurables expérimentalement en collisions électron-noyau au futur EIC ou en collision proton-noyau au RHIC et au LHC, de façon à ce qu'elles soient particulièrement sensibles à Qs, sans être polluées par d'autres effets qui pourraient noyer la signature de la présence du condensat de verre de couleur. Une fois que de telles observables font consensus dans la communauté, il devient alors crucial de les calculer avec le plus de précisions possibles dans le cadre de la chromodynamique quantique, la théorie quantique de l'interaction forte, afin de déduire de façon non ambigüe le signal de la saturation en gluons dans les nucléons.

À l’aube d'une nouvelle génération d’expériences, notamment avec la construction de l'Electron-Ion Collider ou l'installation du détecteur FoCal au sein de l'expérience ALICE au LHC [6], la chromodynamique quantique à haute énergie entre dans une phase d’exploration sans précédent. La décennie à venir promet non seulement des découvertes majeures, mais aussi un renouvellement profond des questions que nous nous posons sur la nature intime et les manifestations les plus extrêmes de la matière hadronique.

Références

1. Quantum Chromodynamics at High Energy, Y. V. Kovchegov, E. Levin, Cambridge Monographs on particle physics, nuclear physics and cosmology,  Cambridge University Press, 2012.
2. The Color Glass Condensate, F. Gelis, E. Iancu, J. Jalilian-Marian, R. Venugopalan, Ann. Rev. Nucl. Part. Sci. 60 (2010), 463-489, https://arxiv.org/pdf/1002.0333.
3. Combined Measurement and QCD Analysis of the Inclusive e+p Scattering Cross Sections at HERA, H1 and ZEUS Collaborations, JHEP 01 (2010) 109, https://arxiv.org/pdf/0911.0884.
4. Evidence for Nonlinear Gluon Effects in QCD and Their Mass Number Dependence at STAR, STAR collaboration, Phys. Rev. Lett. 129 (2022) 9, 092501, https://arxiv.org/pdf/2111.10396.
5. Electron Ion Collider: The Next QCD Frontier : Understanding the glue that binds us all, Accardi et al.,  Eur.Phys.J.A 52 (2016) 9, 268, https://arxiv.org/pdf/1212.1701.
6. A Forward Calorimeter (FoCal) in the ALICE experiment, ALICE Collaboration,  2019, https://cds.cern.ch/record/2696471 .
7. Mining for Gluon Saturation at Colliders, A. Morreale, F. Salazar, Universe 7 (2021) 8, 312, https://arxiv.org/pdf/2108.08254.
8. Nuclear Cold QCD: Review and Future Strategy, Arleo et al., Phys. Rev. C, 2025, https://arxiv.org/pdf/2506.17454.